Limited
Evolutionary Potential
Sean
D. Pitman M.D.
©
November 2006
The
Claim
Michael
Behe, professor of biochemistry at Lehigh University, boldly claims that,
"Molecular evolution is not based on scientific authority.
There is no publication in the scientific literature in prestigious
journals, specialty journals, or books that describe how molecular evolution of
any real, complex, biochemical system either did occur or even might have
occurred. There are assertions that
such evolution occurred, but absolutely none are supported by pertinent
experiments or calculations." 1
The
Controversy
Since
the publishing of Behe's book, Darwin's
Black Box in 1996, a fair bit of controversy has arisen over such
statements. Surprisingly, many
evolutionary scientists seem to grudgingly agree with Behe, at least in some
limited way. For example, microbiologist James Shapiro of
the University of Chicago declared in National Review that, "There
are no detailed Darwinian accounts for the evolution of any fundamental
biochemical or cellular system, only a variety of wishful speculations"
(Shapiro 1996). In Nature, University of Chicago evolutionary
biologist, Jerry Coyne, noted that, "There is no doubt that the pathways
described by Behe are dauntingly complex, and their evolution will be hard to
unravel. . . . [W]e may forever be unable to envisage the first
proto-pathways" (Coyne 1996). In Trends in Ecology and Evolution
Tom Cavalier-Smith, an evolutionary biologist at the University of British
Columbia, wrote, "For none of the cases mentioned by Behe is there yet a
comprehensive and detailed explanation of the probable steps in the evolution of
the observed complexity. The problems have indeed been sorely neglected--though
Behe repeatedly exaggerates this neglect with such hyperboles as 'an eerie and
complete silence'" (Cavalier-Smith 1997). Evolutionary biologist,
Andrew Pomiankowski, agreed. In New Scientist, he challenged anyone to,
"Pick up any biochemistry textbook, and you will find perhaps two or three
references to evolution. Turn to one of these and you will be lucky to find
anything better than 'evolution selects the fittest molecules for their
biological function'" (Pomiankowski 1996). In American Scientist,
Yale molecular biologist, Robert Dorit, suggested that, "In a narrow sense,
Behe is correct when he argues that we do not yet fully understand the evolution
of the flagellar motor or the blood clotting cascade" (Dorit 1997). 7
Observing
the Evolution of a Complex System
Obviously
though, there are many more scientists who passionately disagree with Behe's
position. These scientists argue quite strongly that the mechanism is
known in detail and that it is observed in action all the time producing
"irreducibly complex" systems with complex specified information.
Perhaps one of Behe's
better opponents is Kenneth Miller (biologist, Brown University).
In his 1999 book, Finding
Darwin's God, one of Miller's challenges of Behe's position includes a
1982 research study by professor Barry Hall, an biologist from the
University of Rochester.
What
Hall did was indeed very interesting. He
deleted a gene (lacZ) in a type of bacteria (E.
coli) that makes a lactase enzyme (galactosidase).
This lactase enzyme converts a sugar called lactose into the sugars
glucose and galactose. E.
coli then process glucose and galactose further to extract energy.
One might think that when Hall deleted the gene that codes for the
lactase enzyme that these bacteria would never be able to use lactose for energy
again. However, when Hall exposed
the mutant bacteria to lactose enriched growth media, that they quickly
modified a different gene, which Hall named the "evolved Beta-galactosidase
gene" (ebg), to produce a pretty good lactase enzyme.
This is interesting because the original gene product did not have the lactase
function. Only after a key random mutation was this genetic sequence able
to produce a protein with the lactase function.2, 3
Behe
counters by arguing that as far as the active sites of the lac and
ebg Beta-galactosidase enzymes are concerned, that they are
essentially the same with both being a part of a family of highly conserved Beta-galactosidases
- identical at 13 of 15 active-site amino acid residues. The two mutations
in the ebg Beta-galactosidase, that increase its ability
to hydrolyze lactose, change the two non-identical residues back to those of the
other Beta-galactosidases. So, before the evolution of the lactase
ability of the ebg gene, its active site was already a near duplicate of
other Beta-galactosidases.8
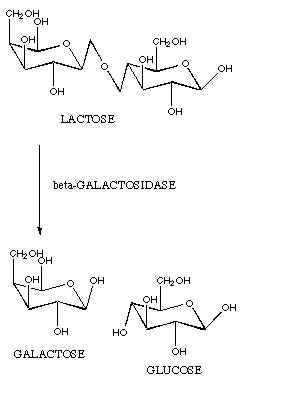Even so, this really was quite an amazing experiment in that a novel
enzymatic function, which was not present in the entire gene pool prior
random mutation and natural selection, did in fact evolve in real time.
According to Miller and Hall, and many others quoting the same or similar
experiments, such experiments give demonstrable proof of the proposed
evolutionary mechanism in action. Obviously
then, Behe does not know what he is talking about . . . or does he? Consider
that fairly often things are not quite as they would appear at first glance.
At
First Glance
At
first glance, Hall's experiment does indeed seem to be a "real time"
example of improvement through mutation and natural selection.
Obviously then, this is evolution in action. Certainly it is, but
it might be a bit different from what one might expect.
It
is not a difficult thing to evolve a particular function if that function is
only one point mutation (one step) away from realization. The odds that one
particular point mutation will happen rapidly in an average sized bacterial
colony are extremely good. A random step/mutation across such a small gap isn't
a problem at all. The real question is, what are the odds that such a
potentially beneficial protein-based structure will actually exist in the
potential of sequence space just one step away from what is currently present
within a given genome? It is this question that those like Hall and Miller
and other evolutionary scientists do not address.
However,
if a small crack in the evolutionary sidewalk can be crossed, why can't these
cracks be added up over time, one new little function at a time, until we end up
with the awesome complexity and variations of life forms that we see today? After
all, the
theory of evolution is based on a fairly simple idea that random mutations
create diversity while natural selection acts as a guide to select those changes
that best aid the survival of that gene pool. Thus, evolution, when it
happens, is not truly a random process - although random events are involved in
the process. Natural selection guides the changes over time, adding them
together, one by one, until the vast diversity of life forms that we see today
is the result. Certainly then, it should at least be technically possible
to add even the smallest changes together over time to produce all the variety
in life forms and functionally complex biofunctions that we see in the world today. Certainly this sounds like
quite a reasonable possibility - at first glance.
A
Closer Look
Most
descriptions of Hall's experiments end with E. coli evolving the lactase function back again. This is
very interesting because Hall's actual experiments did not end there.
After his initial success, Hall wondered if any other genes would be able to
evolve the lactase function. So, he deleted the ebg gene as well as
the lacZ genes to test this hypothesis. And, something most
interesting happened - nothing. No new gene or portion of DNA evolved the
lactase function despite tens of thousands of generations of time, a huge
population size, high selection pressure, and a high mutation rate. Now
that is just fascinating . . .
In
order to understand what happened, lets consider Hall's experiment in just
a little more detail. Behe summarizes Hall's
methods pretty well in the following description:
Without
Beta-galactosidase, Hall's cells could not grow when cultured on a medium
containing only lactose as a carbon source. However, when grown on a plate
that also included alternative, useable nutrients, bacterial colonies could
be established. When the other nutrients were exhausted the colonies stopped
growing. However, Hall noticed that after several days to several weeks,
hyphae grew on some of the colonies. Upon isolating cells from the hyphae,
Hall saw that they frequently had two mutations, one of which was in a gene
for a protein he called "evolved Beta-galactosidase," ("ebg")
which allowed it to metabolize lactose efficiently. (Despite considerable
efforts by Hall to determine it, the natural function of ebg
remains unknown) (Hall 1999). The ebg
gene is located in another operon, distant from the lac
operon, and is under the control of its own repressor protein. The second
mutation Hall found was always in the gene for the ebg
repressor protein, which caused the repressor to bind lactose with
sufficient strength to de-repress the ebg
operon.
The
fact that there were two separate mutations in different genes—neither of
which by itself allowed cell growth (Hall 1982a) - startled Hall, who knew
that the odds against the mutations appearing randomly and independently
were prohibitive (Hall 1982b). Hall's results and similar results from
other laboratories led to research in the area dubbed "adaptive
mutations." (Cairns 1998; Foster 1999; Hall 1998; McFadden and Al Khalili
1999; Shapiro 1997)
As
Hall later wrote, "Adaptive
mutations are mutations that occur in nondividing or slowly dividing cells
during prolonged nonlethal selection, and that appear to be specific to the
challenge of the selection in the sense that the only mutations that arise
are those that provide a growth advantage to the cell. The issue of the
specificity has been controversial because it violates our most basic
assumptions about the randomness of mutations with respect to their effect
on the cell." (Hall 1997) 8
In
short, Hall did in fact delete the lacZ gene (as well as other lac
genes with other related functions) in E. coli bacteria.
These mutant bacteria then evolved the ability to use lactose over a very
short period of time in a non-lethal lactose enriched environment.
They were able to do this with the use of a very fortuitous "spare tire" gene (ebg)
that, with a single point mutation, was able to achieve enough lactase activity
to give the cell a selective survival/reproductive advantage (a second mutation was also required in
the promoter region, but this will be discussed in more detail below).
What
are the Odds?
What are the odds?! That is the real question here. What is the
likelihood that some portion of the collective E. coli genome in a
particular colony of 10 billion would be so close to producing a protein
structure with a particular function, or
any other beneficial function at an equivalent level of functional complexity?
How often would this happen? - on average? Would different types of
functions require different minimum sequence size or degrees of specificity with
regard the the specific arrangement of the amino acid residue
"parts"? If so, would greater minimum size and/or specificity
requirements result in differences in the likely gap distance between what
exists in a genome and what might be beneficial if it were ever found via a
random search through the vast potential of sequence space?
In order to begin answering this question, it might be a good idea to take a
closer look at the actual genetic sequences involved with this experiment.
The lacZ gene is quite long. It consists of approximately 3,500
base pairs in the DNA molecule. This gene codes for a protein that is also
fairly long for proteins (~ 1,000 amino acids). This protein then combines
with three other identical proteins to form a large "tetramer" protein of
approximately 4,000 amino acids (see illustration).4 The
complexity of this lacZ gene would seem to be quite evident. The
level of size and apparent complexity of the ebg gene is similar.
Appearances
can be deceiving though. Maybe lactose hydrolysis is not really as
complicated as the size of this gene makes it appear? As it turns out, a BLAST
search through the known protein databases quickly shows that the smallest known
functional lactase enzyme in any creature is about 380 amino acid residues in size.
Some of these residues also seem to carry with them a fair degree of sequence
specificity. However, many of the residue positions can change, and some of them
can change dramatically, without a significant loss of lactase function.
But, overall, the changeability of the lactase enzyme is at least moderately limited.
Some have suggested to me that there are around 10100 potential
lactase enzymes in all of sequence space made up of chains of proteins
containing 380 residues. Although 10100 does sound like an
absolutely huge number (only 1080 total atoms in the entire
universe), it is actually rather tiny when compared to the total
size of sequence space (~10494 possible combinations for a string of just
380 amino acid residues). With this ratio, for every 1 lactase enzyme, there are
about 10394 non-lactase sequences.
A
Game of Checkers
The
potential of "sequence space" can be visualized as a
gigantic checkerboard. Each square on the checkerboard represents a
different amino acid residue sequence. Each member of a population can
only occupy one square at a time (though any one square may be occupied by many
individuals at any one time). A limited population simply cannot cover all
the potential squares on the checkerboard at any given moment of time.
With each mutation to an individual, it changes squares. If any one
individual comes across a beneficial sequence square, like a residues sequence
with the lactase enzyme function while in a lactose rich environment, that individual and its offspring will tend to stay on that square
because of the selective advantage given by that square in a lactose rich
environment. This advantage will be translated into increased population
numbers that are on and immediately around that particular square of the
checkerboard. Eventually, in a steady state population, the entire
population will be around that one square because they will all be descendants
of the original individual that first came across that beneficial square on the
checkerboard.
The
problem is that not every square is beneficial. Depending upon the level
of functional complexity in question, most squares are completely neutral for
survival and many more are detrimental. So, in traveling from one
beneficial square to another beneficial square at the same level or even a higher enzymatic level of
complexity, an open ocean of non-beneficial sequences will have to be crossed.
The problem with this open ocean is that during this voyage over neutral waters,
natural selection cannot direct the process at all. Nature is blind to
such voyages and so the process becomes purely random. In fact, this
voyage has a mathematical name called "random walk" which does in fact
occur in real life (i.e., Kimura's Neutral Theory of Evolution).
The
interesting thing about random walk is that with each doubling of the distance
length to the average beneficial sequence square on our checkerboard, the time
involved increases exponentially. For example, if the average random
walk required for a particular colony of bacteria to achieve a particular level
of complexity required 5 neutral steps or changes in DNA, the total number of
options or potential spaces on our checkerboard between the starting point and a
new "winning" square would be 4 (remember that there are four
potential bases that can fill one given location in a string of DNA) to the
power of 5, or 1,024 squares. So, the random walk would not simply take 5 steps
in a straight line to the new beneficial square. Not at all. The
random walk would wander randomly or blindly around 1,024 squares, taking far
more steps, on average, to find the one square out of 1,024 that is actually
selectable as "beneficial" to those that are searching the sequence
space of that checkerboard. Depending
on our population's size and mutation rate, we could estimate an average time
required to reach all of these squares at least once beginning at a given starting point. Obviously though, the bigger the population and the higher
the mutation rate, the faster random walk could reach all of the squares.
For
instance, if we started out with a population of 1 trillion bacteria and if all
of these bacteria started out on one square on our checkerboard, it would take
around 65,000 generations (if each individual sequence of a given length was
mutated at least once in each generation) for them to reach equilibrium over all
the squares of the checkerboard - kind of like a tall column of sand being let
loose at one location and then rapidly flowing and spreading itself in all
directions to other locations. At equilibrium (i.e., when the pile of sand
becomes perfectly "flat" or evenly distributed over all surfaces),
about 0.098% of the bacteria will be on each one of the 1,024 squares of the
checkerboard. Even though 0.098% does not really seem like a big number,
it actually works out to be around 9.8 billion out of a population of 1
trillion. In other words, after about 65,000 generations, there would be
an average of 9.8 billion bacteria covering each one of the 1,024 squares on our
checkerboard of potential space.
So
obviously, a gap of 5 neutral mutations would not be a problem for a population
of 1 trillion bacteria to cross in relatively short order. But, what
happens if we double the gap to 10? A gap of 10 neutral mutations/steps
would create a checkerboard with over 1 million squares of potential space
(1,048,576 to be exact). At equilibrium, our population of 1 trillion
would have only 953,674 individuals on each of the squares instead of the 98
billion it had when the gap averaged only 5 steps wide. Doubling the gap
again to 20 steps makes our checkerboard grow a million fold to just over 1
trillion squares of potential space (1,099,511,627,776). Now, our
population of 1 trillion would average a bit less than one member of the
population on any one square at any given point in time. I think the trend
is obvious by now, but just for kicks, doubling the gap again to 40 steps
increases the size of our checkerboard a trillion fold to just over 1 trillion
trillion squares. Now, at equilibrium, each one of the members of our
population of one trillion are surrounded, on average, by one trillion empty
squares that they have to search out all by themselves.
Average
Time
Take
a population of bacteria the size of all the bacteria that currently exist on
the entire Earth - about 1e30 bacteria. Let's say that this steady state
population produces a new generation at a rate of 20 minutes and has a mutation
rate of 1e-8 per codon position - given a genome per bacterium of 10 million
codons. How long would it take such a population to find a new beneficial
function at the level of 1,000 fairly specified residues?
Well,
first we have to calculate the likely gap size. Using an average between
the calculations of Yockey and Sauer, the ratio of potential beneficial vs.
non-beneficial for 100aa systems is about 1e-40.13,14,15 This
creates a ratio for a 1,000aa system of about 1e-40(1000/100) =
1e-400. So, the average gap size between potentially beneficial sequences at
this level would be about 308 residue differences - i.e., 20308
= 1e400.
At
his point, one can calculate the Poisson
distribution curve to determine the odds that any particular gap would exist
(given the average gap of 308 residue differences). Although extremely unlikely
given the Poisson distribution, let's say that our colony has a few closer
sequences that just aren't "average" - close enough to be only 50
specific residue changes away from at least one beneficial function at this
level of minimum size and specificity. How long would it take to get just
50 specific residue changes?
A
gap of 50 specific residue differences from a given 1,000aa sequence means that
each of these sequences is surrounded by 1e65 non-beneficial options. But,
we have 1e30 bacteria with 1e7 codons each. For arguments sake, lets say
that each bacterium has 1e5 sequences of 1,000 codons that are within 50 residue
changes of success. This gives us a total population of 1e35 starting
points that are within 50 changes of success.
Now,
how long will it take to get these 50 needed changes in at least one bacterium
in our population? After equilibrium of distribution randomly through
sequence space is realized, each one of our starting point sequences must search
through a sequence space of 1e65/1e35 = ~1e30 sequences, on average, before
success will be realized. With a mutation rate of 1e-8 per codon per
generation our 1,000-codon sequence will get mutated once every 1e5 generations.
With a generation time of 20 minutes one mutational step takes about
2,000,000 minutes or approximately 4 years. So, with one random walk step every
4 years, it would take 1e30 * 4 = 4e30 years to achieve success - on average
(i.e., trillions upon trillions of years).
Evolution
Stalling Out
With each doubling of the
likely neutral
gap, the average time required for "success" increases exponentially. Of course, one way to reduce the
average required time is to increase the
population's size exponentially. This does help for a while, but very
quickly the required size of the population becomes impractical for any
environment to support and further evolution simply stalls out, in an
exponential manner, with attempts to reach higher and higher levels of
functional complexity. Interestingly
enough, Barry Hall discusses this very problem:
Given
a gene of 1000 base pairs there are over 1034 sequences that differ
from the wild-type sequences by 10 or fewer mutations. Not only can we not
explore all of those possible variants, life itself has barely had sufficient
time to explore all of those possibilities. The mass of the earth's oceans is
about 1.4 x 1024g. Even if living cells constituted a 10-4
of the mass of the oceans, given about 1012 bacterial cells per
gram, a reproduction rate of about 1 cell generation per day and a mutation
rate of about 10-9 per cell generation and 4 billion years of life
there has been sufficient time to explore only 1.6 x 1034 variants
of a single 1000-bp sequence. However, evolution does not proceed by exploring
all possible variants but by incorporating single mutations, selecting the
fittest of those variants, expanding the population of the fittest variants,
and incorporating additional single changes.
Hall
goes on to explain: If the evolved sequence differs from the
wild-type at n sites there are n possible first-step amino acid replacement
mutants. Each of those single mutants can be created by site directed
mutagenesis and the effect on fitness determined by competition experiments.
The best (fittest) of those amino acid replacements can be chosen and the n31
possible second-step mutants created, the fittest double mutant chosen, the
n32 possible third-step mutations introduced, etc. The effect of this exercise
is to mimic an evolutionary pathway in which the fittest single mutant is
fixed into the population, that population expands, the fittest double mutant
arises and is fixed into the population, etc. Orr has recently shown on
theoretical grounds that adaptive evolution is expected to proceed in exactly
this fashion in which the first mutations to be fixed are those that have the
greatest positive effect. 9
Of
course, all of Hall's single steps here are functionally beneficial. What
happens if there are true gaps in function? What happens to evolution? Hall
continues:
If
that sequence involves six amino acid replacements, we might find that after
introducing three replacements, each of which further improves fitness, none
of the three remaining replacements improves fitness. Assuming that the final
six-mutant sequence is significantly fitter than the triple mutant, that
result means that two, or perhaps even three, of the remaining substitutions
must be introduced simultaneously to further improve fitness. This
simultaneous occurrence of two or more specific mutations is obviously highly
unlikely, but what about the possibility that one of the two mutations will
arise, by selectively neutral, but be fixed into the population by drift? Were
that to occur the second mutation would quickly be incorporated by selection.
The probability that a newly arisen neutral mutation will be fixed into the
population is the reciprocal of the population size. When populations are
large enough that the probability of the occurrence of the mutation is very
high, e.g., the population size approaches the reciprocal of the spontaneous
mutation rate, then the probability of the fixation is very low. Although
neutral variants arise constantly, it is very unlikely that the particular
neutral variant we require will be fixed into the population. Thus, unless
each of the mutations confers a selective advantage relative to its parent, it
is unlikely that the final six-mutant sequence would evolve naturally. In the
example above we would conclude that the evolutionary potential may well be
limited to the triple mutant. 9
So, even Hall admits that very small neutral gaps of three mutations might
be enough to "limit" further evolution. Thus, such functions that are
isolated from other functions by neutral gaps might be quite difficult for a
theory based on the mechanism of random mutation and function-based
"natural" selection to explain.
Humpty
Dumpty Had a Great Fall
What
is also most interesting is that the same bacteria that couldn't evolve a
relatively simple single protein enzymatic function, like lactase (i.e., Hall's
double mutant E. coli), would quickly evolve
resistance to any modern antibiotic in short order via random mutation and
natural selection. Why then is it so easy to evolve antibiotic
resistance but not a beneficial enzyme starting with what is currently
available in the collective genome? Well, perhaps it is because functions
are not created equal. Some functions are extremely simple while others
are vastly more complex (i.e., in both the minimum length requirement of a coded
sequence or number of required parts as well as the minimum degree of specified
arrangement of the sequence or types of parts).
De novo antibiotic
resistance is one of the most simple functions around. The reason for this
can be found in the specificity of a given antibiotic for a particular target
within a bacterium. Because of this high specificity, there is a
very high ratio of potentially "beneficial" changes compared to
"non-beneficial" changes that can in fact interfere with such specific
interactions of molecules. The neutral gap involved in finding at least
one of these very common potential interfering sequences is quite small indeed.
Perhaps, in some cases, a majority of mutations would result in interference
with such a specific interaction. Obviously then, when an interfering
mutation does come along that blocks or completely destroys the interaction of
an antibiotic with its specified target, the antibiotic resistance function is
evolved. It is much like the breaking of Humpty Dumpty when he fell off
the wall. He broke easily because there are so many ways he could be
"broken". However, it wasn't so easy to put him back together
again because the vast majority of potential ways to arrange his parts just
won't "work" - and that's the catch for the theory of evolution.
Functions
that are based on the destruction or interference with other pre-formed
functions or interactions are universally very simple to evolve. This is
mathematically predictable and in real life it does in fact occur quite
commonly. Antibiotic resistance evolves very rapidly in real life even
without access to such complex antibiotic enzymes like penicillinase (which has
never been shown to evolve in real time by the way). A few other types of
drug resistance, such as chloroquine resistance, have taken a bit longer to
evolve in real life (though never in laboratory conditions), but even this type
of evolution works on the same basis of interference with a preformed function.
Chloroquine
resistance (CQR) seems to require at least a few mutations (as many as 6, but
perhaps only two mutations), before at least some beneficial level of resistance
can be realized. It turns out that several of the mutations seen in CQR are
selectively advantageous once the initial two or three are realized.
Resistance to both mefloquine and chloroquine is achieved via the blocking of or
interference with a pre-established interaction of these drugs with specific
target proteins.
Again,
the prediction that such interferences are relatively easy to achieve holds up
in these cases as well. No new protein or enzyme is evolved in these cases. The
only thing that happens is a disruption of a specific interaction that was
pre-established. It is just a different way of breaking Humpty Dumpty, but
still relatively easy to do with large populations. This evidence fits very well
with my predictions for the required time needed to evolve functions at this very low level
of complexity (more of the details of chloroquine resistance in the reference section below).10
Climbing
the Ladder of Functional Complexity
However,
as one moves up the ladder of complexity to those functions that are not based
on interference with pre-established functions (single protein enzymes like
lactase, nylonase, penicillinase, etc), the relative number of such
sequences is dramatically reduced. This makes the evolution of such
functions much more
difficult and, in real life, there are far fewer examples at this level of
functional complexity. Certainly the evolution of lactase, nylonase,
and several other single protein enzymes that have been demonstrated in real
life are definite examples of higher-order evolution in action when compared to
the extremely simple function of antibiotic resistance and other such functions. However,
there are far fewer examples at this level, relatively speaking, And, there are
very interesting limitations at this level - as illustrated in Hall's
experiments with lactase evolution in E. coli.
Evidence
for this position can be found in the fact that all bacteria can and do rapidly
evolve antibiotic resistance to any antibiotic that is brought their way.
However, only a very few of them can evolve new enzymatic activities, such as a
relatively simple lactase function provided by any one of literally trillions
upon trillions of potential lactase enzymes dispersed through sequence
space.
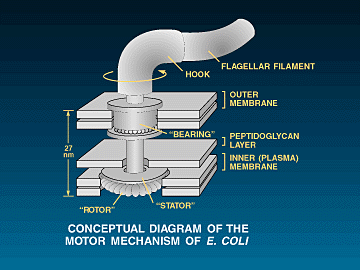Of
course, there are even higher levels of complexity that involve multiple
proteins all working together at the same time in order for a particular
function to be realized. A classic example of such a level of function can
be found in bacterial
motility systems. All bacterial motility systems are dependent upon
the simultaneous action of many different proteins all working together
in harmony in specific orientation with each other. A common example of such a motility system is the flagellar
system of motility. The flagellar system requires around 50 genes to
construct and regulate the eubacterial flagellum and around around 18-20 fairly specified
proteins (averaging around 300 residues each), to form the actual motor-switch-shaft-propeller complex.
![]()
The
flagellum is in fact a biochemical machine that does very much resemble
something a human would design. There is the helical filament (propeller),
the hook (universal joint), the rod (drive shaft), the S-P ring (bushing around
the rod - in gram negative bacteria), the SMC ring complex, and the
"motor" which includes the stator and the rotor. The entire assembly
is hollow, including the actual filament. The rotor, hook and filament are made
of different helical proteins that self assemble to form hollow, cylindrical
structures (in the case of the filament, the cylinder is helical so that it acts
as a "screw propeller" when it rotates. Also, many eubacteria
can switch the direction of rotation of the propeller (and hence the direction
of travel) and the "switch" mechanism appears to be part of the
motor complex (More detail is listed below in
the reference section as well as in another essay of mine dealing specifically with the flagellum).
1, 11
Minimum
Number and Specificity of Parts
Without
a minimum number of parts being present in the proper "specified"
order and orientation, the function of motility could not be realized, even a
little bit. Many, like biologist Kenneth Miller, argue that such multi-part systems of function are made up of
less complex sub-systems of function that have other functions within the cell -
meaning that they are not truly "irreducibly complex".
The argument is made that several of the flagellar sub-structural proteins and
even systems of protein parts have homologues in other independently functional
cellular systems. One well-known example is a secretory system called the
"Type III protein secretion system" or "TTSS". Interestingly enough, some
of the parts used in the secretory systems of some species are nearly identical
to some of the parts used in the flagellar motility system (More detail
in reference section and flagellum
paper).11 Of course, the object of such
arguments is to suggest that as long as all the needed sub-parts are there, that
a beneficial apparatus of higher functional complexity, like the flagellar
motility system, will obviously self-assemble, eventually, when needed.
There
are several potential problems with this hypothesis however. Perhaps the
most obvious problem is the fact that no such demonstrations of the evolution of
multiprotein systems of function have ever been observed or even theorized in a
falsifiable way when they require more than a few hundred fairly specified amino
acids working together at the same time (i.e., the multiprotein flagellar system
of motility requires a minimum of several thousand specifically arranged amino
acid residues, working together at the same time). Lower
levels of functional complexity, that involve interference with pre-established
functions (antibiotic resistance) or that are based on single protein enzymes
(lactase, nylonase, etc), have been shown to spontaneously evolve.
However, no function at a higher level of complexity, that involves multiple
proteins totaling more than a few hundred fairly specified residues, has ever
been shown to evolve in real time. There isn't a single published example.
It is here that Behe is
correct in saying that no such system of function has been or likely can be
explained through evolutionary mechanisms of "random mutation combined with
natural selection".
Also,
just because all the necessary parts are available, in close proximity, to form
a potentially beneficial system does not mean that the parts will
"know" how to spontaneously self-assemble to form such a beneficial
system if each intermediate step is not also more "beneficial" than
that which came before. And, we know that the intermediate steps are not
all beneficial when in comes to the functional systems of living things.
In fact, we know that the large majority of all potential changes to both
functional as well as non-functional DNA are neutral at best and, if functional,
are almost always detrimental. This becomes more and more true at higher
and higher levels of functional complexity due to the exponential growth of
neutral gaps with each step up the ladder of functional complexity.
All
Functions are "Irreducibly Complex"
The
fact is that all cellular functions are irreducibly complex in that all
of them require a minimum number of parts in a particular order or orientation.
I go beyond what Behe proposes and make the suggestion that even single-protein
enzymes are irreducibly complex. A minimum number of parts in the form of
amino acid residues are required for them to have their particular functions. The
lactase function cannot be realized in even the smallest degree with a string of
only 5 or 10 or even 100 residues of any arrangement. Also, not only is a
minimum number of parts required for the lactase function to be realized,
but the
parts themselves, once they are available in the proper number, must be
assembled in the proper order and three-dimensional orientation. Brought
together randomly, the residues, if left to themselves, do not know how to
self-assemble themselves to form a much of anything as far as a functional
system that even comes close to the level of complexity of a even a relatively
simple function like a lactase enzyme. And yet, their specified assembly
and ultimate order is vital to function.
Of
course, such relatively simply systems, though truly irreducibly complex, have
evolved. This is because the sequence space at such relatively low levels
of functional complexity is fairly dense. It is fairly easy to come across
new beneficial sequences if the density of potentially beneficial sequences in
sequence space is relatively high. This density does in fact get higher and higher at
lower and lower levels of functional complexity - in an exponential manner.
It is much like
moving between 3-letter words in the English language system. Since the ratio of meaningful vs. meaningless
3-letter words in the English language is somewhere around 1:18, one can
randomly find a new meaningful and even beneficial 3-letter word via single random
letter changes/mutations in relatively short order. This is not true for
those ideas/functions/meanings that require more and more letters. For
example, the ratio of meaningful vs. meaningless 7-letter words and combinations
of smaller words equaling 7-letters is far far lower at about 1 in 250,000.
It is therefore just a bit harder to evolve between 7-letter words, one mutation
at a time, than it was to evolve between 3-letter words owing to the exponential
decline in the ratio of meaningful vs. meaningless sequences.
The
same thing is true for the evolution of codes, information systems, and systems
of function in living things as it is for non-living things (i.e., computer
systems etc). The parts of these codes and systems of function, if
brought together randomly, simply do not have enough meaningful information to
do much of anything. So, how are they brought together in living things to form
such high level functional order?
Limited
Evolutionary Potential
And yet, despite these many problems, professors Hall and Miller and many other
scientists like them would have us believe that the evolution of even more
complex functions than single protein enzymes is still a relatively simple or at
least a doable process given a few million or even billion years. Such
conclusions might be a bit premature to say the least since many of Hall's
mutant E. coli seemed to have more than a little difficulty evolving just
one relatively simple single-protein enzymatic function. Hall himself
described these strains as having "limited evolutionary potential." 3
Hall noted that with both the lacZ and the ebg genes missing, E.
coli bacteria cannot evolve lactase ability at all despite his own efforts
and those of several others, such as J. H. Campbell, to test for and observe
such evolution over the course of many years (since 1973) totaling hundreds of
thousands of bacterial generations.6
Hall did seem to realize somewhat of the implications of discovering that only
one mutation was needed to "evolve" efficient lactase activity in lacZ
negative E. coli strains. In his paper he said, "The realization
that a single mutation in ebgA [ebg =
evolved b-galactosidase gene] was sufficient to convert ebg0 enzyme
into an efficient lactase was therefore disappointing." 3
The problem, as Hall himself pointed out, is that there are
mutations that do not yield changes in protein function toward anything useful
to the cell. The proteins that result from these mutations might in fact
be useful to another organism somewhere in the universe, but for the particular
organism that they have evolved in, they are either neutral in function or
nonfunctional . . . or, even worse, detrimental in function.
No cell or organism or even an entire gene pool has an infinite vocabulary.
All living things have limited individual vocabularies. Out of the huge
number of possibilities for different kinds of proteins of a given length, any
one individual cell or gene pool of cells "recognizes" or can use only
a small fraction of them in a beneficial way (and this fraction gets
exponentially smaller as the level of complexity increases). Therefore,
some functions are in fact out of statistical reach for that particular cell, or
gene pool of cells, as well as their offspring because they do not recognize, as
beneficial, any change in the functions of intermediary proteins along the way
toward those sequences that would in fact be beneficial. Such neutral
evolution looses the guidance of natural selection as a driving force.
Hall describes such evolutionarily-challenged bacterial strains as having "limited evolutionary potential." I propose that every living creature
has very limited evolutionary potential.
Bridges
Between Old and New Functions
Some might argue that some
of the changes described by Hall did in fact cross bridges of non-function.
This is true. Hall described the crossing a nonfunctional bridge that was
two mutations wide. Hall found even this challenge statistically unlikely,
but it did in fact happen experimentally. The statistical problem Hall
describes is that for each genetic change in function, a change in regulator
function is also needed. A regulator is needed to control the production
of the regulated gene. Without regulation, genetic products are not
advantageous and will be selected against in later generations. The needed
lactase regulator change also required, in this case, a single point mutation
that was in line with the single lactase gene point mutation.
Independently, the statistical odds of the needed genetic mutation happening in
a given bacterium, according to Hall, was 2 x 10-9 and the
statistical odds for the needed mutation in the regulator region of that gene is
1 x 10-8 (at best). The generation time for Hall's bacterial
cultures averaged 6 hours and the average number of bacteria that were being
studied at any given steady state was at best 1010 cells.
According to Hall's own statistical calculations, the average time required
for both of these needed mutations to occur in any one of his bacterial colonies
was on the order of 100,000 years.
It seems though that Hall's math was a bit off. According to the
statistics of random walk in a population of 10 billion, a gap of two mutations
(only 16 squares to cover on our checkerboard) would be crossed in short order -
and it was crossed in short order. According to Hall, colonies containing
both of these mutations were isolated in as little as nine days. However,
because of Hall's calculations (based on the requirement of full fixation of the
first "correct" mutation in the colony before a gain of the second
"correct" mutation) and estimates of much more time to achieve such a
crossing, Hall concluded that, "under some conditions spontaneous mutations
are not independent events." He went on to say that this is
"heresy, I am aware." 3
Because of his statistical
calculations, Hall was forced to conclude that mutations are not always random
events but that sometimes point mutations occur in tandem at a higher rate than
random chance alone would allow. Of course there was no logical
explanation for this assumption, and yet Hall assumed that was is in fact what
was happening. He felt forced to conclude that nature seems to know what
it wants ahead of time and manipulates mutations without the aid of any
functional advantage. Truly, this is scientific heresy as Hall indicates.
It is basically a statement of magic. Of course, Hall was wrong.
Random walk in such a large bacterial population can easily cross a gap of 2 or
3 or several more mutations in very short order, but what is there that explains
the existence of gaps that average hundreds, thousands, or even millions of
mutations wide? Magic? - or intelligent design?
Statistical
Road Kill
Miller and Hall have failed to defeat Behe's argument of irreducible complexity
for one simple reason that Behe describes as statistical "road kill."
As previously described, the road-kill problem is the problem of gaps - gaps of
neutral function. Single point mutations quickly come to gaps of neutral
or even non-function that require multiple mutations to cross. At this
point, evolution is stuck. And yet, we know that these gaps have in fact
been crossed somehow, but how? Obviously something or someone has crossed
them at some point, because genes do in fact exist on the other side of these
gaps. The gaps themselves exclude natural selection as a force that can
fly evolution over to the other side since natural selection is dependent upon
the detection of functional phenotypic change. Without natural selection,
the crossing of these gaps via any naturalistic process remains a mystery.
Random mutation, by itself, tends toward homogeny, not the increase of meaningful
genetic information. Therefore, without guidance, random chance fails as a
creative force of new high-level systems of function because random chance
eventually creates homogeny (i.e., goop).
However, if it is still difficult to see that neutral genetic gaps significantly
limit the powers of Darwinian evolution, consider the Shakespearean phrase,
"Methinks it is like a weasel" used by Richard Dawkins to illustrate the
power of natural selection.12 Try and change any one letter or
space and still have the sentence remain meaningful as well as beneficial in a
given situation/environment. You might change it to read, "Me thinks it
is like a weasel" then, "He thinks it is like a weasel." It still
makes sense and it means something different. Aha! Evolution in
action. Keep going though. How far can you evolve this sentence
where each and every character change remains meaningful much less beneficial?
You might mutate it to, "She thinks it is like a weasel" then, "She thinks
it is like a teasel" then, "She thinks it is like a tease" then,
"He
thinks it is like a tease" then… well… you see, it is getting quite
difficult to keep evolving unique as well as meaningful phrases one mutation at
a time. We run into evolutionary dead
ends really fast.
The same problem happens with genetic "evolution." The genetic
blueprints of living things are written according to very specific rules of
"grammar." The order or sequencing of genes is very important to
function. Not just any order will do. The "spelling" of genetic
words also matters. The cell will not recognize just any spelling as
beneficial in a given environment. So, to go from one functional genetic
phrase to another uniquely functional genetic phrase in a higher level of
functional complexity might be a bit of a problem if such changes require the
crossing of even a few neutral or detrimental steps of random walk.
Each mutation that does not cause a beneficial change in function (i.e., neutral
or detrimental) is one lane in the statistical highway that Behe describes.
The blind turtle of evolution must cross this highway to reach the new
beneficial function. With each additional lane added to the highway, the
average time needed for the blind turtle to make it across increases
exponentially. Each lane that is added skyrockets the average needed time
for success until 4 or 5 billion years pales into the distance of trillions upon
trillions of years.
Given
Enough Time Anything is Possible
There are those who say that evolution is improbable, but that time makes the
improbable - probable. Time becomes the savior of evolution. This
might be true except for one small problem. Evolution needs more time than the
history of the universe, or even millions upon billions upon trillions of
universes have to offer - on average. How high do the odds have to go
before we suspect that all this just isn't the result of any non-deliberate
process? How many times would the same person be able to win the
California Lottery in a row before one could reasonably suspect the possibility
of deliberate cheating?
-
Behe,
Michael J. Darwin's Black Box,
The Free Press, 1996.
-
Miller,
Kenneth R., Finding Darwin’s God,
HarperCollins Publishers, 1999.
-
B.G.
Hall, Evolution on a Petri Dish. The
Evolved Beta-Galactosidase System as a Model for Studying Acquisitive Evolution
in the Laboratory, Evolutionary Biology, 15(1982): 85-150.
-
Lewin,
Benjamin, Genes V, Oxford
University Press, 1994.
-
Levinson,
Warren E. et al., Medical
Microbiology and Immunology 3rd Ed., Appleton & Lange,
1994.
-
Campbel,
J.H., Lengyel, J., and Langridge, J., 1973, Evolution of a second gene for
B-galactosidase in Escherichia coli, proc. Natl. Acad. Sci. USA
70:1841-1845.
-
Behe,
Michael J., Irreducible Complexity and the Evolutionary Literature:
Response to Critics, Discovery Institute, July 2001. (http://www.arn.org/docs/behe/mb_evolutionaryliterature.htm)
-
Behe,
Michael J., "A True Acid Test" - Response to Kenneth Miller,
Discovery Institute, May 2002.
(http://www.trueorigin.org/behe02.asp)
-
Hall,
Barry G., Toward and Understanding of Evolutionary Potential, FEMS
Microbiology Letters 178 (1999) 1-6, June 1999. (http://www.eeb.uconn.edu/Courses/EEB449/Hall%20FEMS.pdf)
-
Jane
MR Carlton, David A Fidock, Abdoulaye Djimdé,Christopher V Plowe and Thomas
E Wellems, Conservation of a novel vacuolar transporter in Plasmodium
species and its central role in chloroquine
resistance of P. falciparum, Current
Opinion in Microbiology, 2001. (http://www.dbbm.fiocruz.br/class/Lecture/d24/drug_resistance/mc4404.pdf)
In
human red blood cells, Plasmodium falciparum (the malaria
parasite) supports its growth by taking up host cell cytoplasm in an acidic
digestive food vacuole. Toxic heme, in its hematin form, is released in the
vacuole by hemoglobin digestion and is crystallized into innocuous hemozoin,
or "malaria pigment". Chloroquine (CQ) interferes with this
process by complexing with hemozoin. This complex prevents hematin from
crystallizing into the innocuous hemozoin form. The "toxic"
effects of free hematin are caused by hematin's ability to increase membrane
permeability which lead to cell lysis and death. Hematin also is known to
inhibit parasite enzymes.
Chloroquine
resistant strains of P. falciparum show a reduced accumulation of CQ
in the digestive vacuole. The genetic mutations associated with this reduced
accumulation have been isolated to the PfCRT (P. falciparum
chloroquine resistance transporter) gene. The gene contains 13 exons that
cover 3.1 kb. The PfCRT gene product is a 423 amino acyl ten-transmembrane
channel or transporter protein that catalyzes chloroquine flux and H+
equilibrium across the digestive vacuole membrane. Many different point
mutations have been isolated in resistant CQR strains of malaria (M74I,
N75E, K76T, A220S, Q271E, N326S, I356T, and R371I). Of these, only the K76T
and the A220S mutations are shared in common between resistant malaria
strains on various affected continents of Asia, Africa, and S. America. The
K76T mutation in particular seems to be the most important marker of CQR.
What is interesting is that the K76T mutation is never seen by itself, but
is always associated with a few other point mutations. However, in some CQ
resistance strains the K76T mutation is absent. One such strain is the
"106/1" strain that has the K76I mutation instead. This strain has
six of the other point mutations, but is has the K76I instead of the K76T
mutation at position 76. Even without the K76T mutation the 106/1 strain
does have a fairly high level of CQR. However, the level of resistance is
not as high as those strains that do have the K76T mutation. Interestingly
enough, Fidock et al., performed an experiment with the 106/1 strain where
stepwise CQ pressure was added to the population. The result was a fairly
rapid change at position 76 from the K76I to the more resistant K76T
mutation.
The
results of such observations suggest that the K76T mutation is not
selectively advantageous by itself. the A220S may fulfill a particular
requirement in the development of CQR since this mutation has consistently
been found to accompany the K76T mutation in CQR parasites from the
different New and Old World foci. "The suggestion that K76T cannot
occur in the absence of other PfCRT point mutations may also explain the
slow genesis of CQ resistance in the field as well as the difficulties that
have been experienced with attempts to select CQ resistance in the
laboratory."11
-
Ian Musgrave, Evolution of the Bacterial Flagella, Personal Website, created in
2000. (http://www.health.adelaide.edu.au/Pharm/Musgrave/essays/flagella.htm)
-
Dawkins, Richard. The Blind Watchmaker,
1987.
-
Yockey,
H.P., J Theor Biol, p. 91, 1981
-
Yockey,
H.P., "Information Theory and Molecular Biology", Cambridge
University Press, 1992
-
Sauer,
R.T. , James U Bowie, John F.R. Olson, and Wendall A. Lim, 1989,
'Proceedings of the National Academy of Science's USA 86, 2152-2156. and
1990, March 16, Science, 247; and, Olson and R.T. Sauer, 'Proteins:
Structure, Function and Genetics', 7:306 - 316, 1990.
Appendix
The
Flagellum:
Propeller:
The Filament (propellor) is composed of the proteins FlaA and FlaB.
Deletion of FlaB doesn't seem to do hinder motility too much and deletion of
FlaA results in trucated flagella which still produce some motility, and
have some motility.
Hook/universal
joint: This is formed by FlgE
proteins and possible a few others. There is very limited sequence
similarity between the FlgE's of Salmonella sp. and Heliobacter
sp. (33% identity).
Drive
Shaft: The rod (driveshaft) is
composed of a complex of the proteins FlgG, FlgB, FlgC, FlgF and FliJ, P, Q,
R. The M ring is formed from FliF proteins. The
L and P rings are composed of proteins FlgH, FlgI, but these can be absent
or present without significant effects on flagella function.
Motor:
The motor consists of a rotor (the part that spins) and the stator (the part
that does the spinning). The motor is largely contained by the C ring motor
complex. This is formed from FliG, FliM, FliN proteins which form the
rotor/switch apparatus. The stator is formed from either MotA and B in some
species, and PomA, PomB, MotX and MotY in others .
Stator:
Mot A and B forms a proton pump which provides the power of the motor, MotB
also serves to anchor the motor to the cell. Deletion of Mot A or B paralyses
the cell. FliG and FliM proteins are also involved.
In
Rhodobacter sphaeroides, the genes equivalent to MotA and MotB have
only 19% sequence identity. The Rhodobacter motor doesn't switch as
does the other motors, but turns on and off, and re-orientation is via
Brownian motion.
In
Vibro species, the motor is a sodium, rather than proton pump,
composed of pomA, pomB, MotX and MotY. The MotX and Y proteins are
unrelated to MotA or B, but PomA seems to be related to MotA from R.
spheroides, and R. spheroides. MotA can partially restore
swimming in PomA paralyzed mutants.
The
rotor: The FliG protein is
involved in torque generation. It turns the proton gradient into
rotational motion in a poorly understood way. It may also have a role in
switching. FliM is also involved in switching, but probably not in torque
generation. FliN is probably not involved directly in
either torque generation or switching, and may be a stabilizing protein. In Bacillus
species it is replaced by the protein FliY, which resembles a fusion between
FliM and FliN.
Homologues:
It is true
that homology studies have shown that many of the flagellar proteins are
related to parts of the type III protein secretion system. Some of these
parts are even identical in some bacterial species. FliN is homologous to the
Spa0 and HrcQ protein export proteins in the Salmonella and Pseudomonas
respectively. FliP,Q,R and F proteins are homologous to HrcR,S,T and J
proteins of the Pseudomonas Hrp type III secretory system, and indeed
have homologues in most type III secretory systems.
The
type III secretory system forms a "rivet" structure identical to the
rod and SMC ring complex of the flagellum. Furthermore, the
switching/torque generation system (FliG,FliN/Y), has homologues in virtually
every type III secretory system examined so far. Proteins exported by
this system are shunted through the hollow SMC ring and through the rod to the
outside of the cell. In flagellum assembly, flagellins and hook proteins
are shunted to the outside of the cell via the rod and ring complex. The
proteins attach to the outer rim of the rod and self assemble into a tubular
structure that will become the hook and filament. The flagellar proteins
then pass through this tube as it grows. However, there is no apparent
homologue of the motor (MotAB) in type III secretory systems. Several of
the type III secretory systems have tubular structures attached to the rod.
The Hrp secretion system forms basal ring/rod system with a pilus that
strongly resembles the flagellar system. It is not clear if the Hrp pilus has
any relation to the flagellar filament. However, E. coli has a
filamentous structure attached to one of its type III secretory systems which
has significant similarity to the flagellar filament.
.
Home Page
. Truth,
the Scientific Method, and Evolution
.
Methinks
it is Like a Weasel
. The
Cat and the Hat - The Evolution of Code
.
Maquiziliducks
- The Language of Evolution
. Defining
Evolution
.
The
God of the Gaps
. Rube
Goldberg Machines
.
Evolving
the Irreducible
. Gregor
Mendel
.
Natural
Selection
. Computer
Evolution
.
The
Chicken or the Egg
. Antibiotic
Resistance
.
The
Immune System
. Pseudogenes
.
Genetic
Phylogeny
. Fossils
and DNA
.
DNA
Mutation Rates
. Donkeys,
Horses, Mules and Evolution
.
The
Fossil Record
. The
Geologic Column
.
Early Man
. The
Human Eye
.
Carbon
14 and Tree Ring Dating
. Radiometric
Dating
.
Amino Acid
Racemization Dating
. The
Steppingstone Problem
.
Quotes
from Scientists
. Ancient
Ice
.
Meaningful
Information
. The
Flagellum
.
Harlen Bretz
. Milankovitch
Cycles
Since
June 1, 2002
